Introduction
This article looks at the magnitude of celestial objects and its relevance to imaging. Many amateur astronomers use the apparent magnitude of a celestial object as a guide to selecting a target in terms of its brightness.
However, this measure only applies to point sources like stars and does not apply to the extended targets like nebulae and galaxies where surface brightness is far more relevant.
For example, an exposure of a few seconds will be more than enough to capture a star of magnitude 10 but an apparently large magnitude 10 galaxy will not even show on the camera sensor as the available light spreads across its surface.
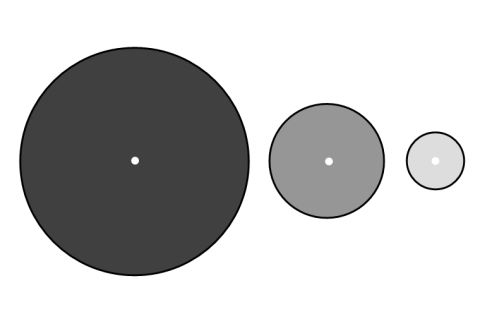
The approximation on the right, illustrates the effect of surface brightness. The image shows three light sources of the same magnitude but of different surface sizes. All three sources emit the same amount of light which is evenly spread over the surface of the light source.
Magnitude
The apparent magnitude of a celestial body is a measure of its brightness as seen from Earth. Brighter objects have lower magnitude values with Vega having a magnitude of 0. The faintest stars visible to the human eye form a dark location is typically 6 where from a suburban location is around 3.
| Magnitude |
Celestial object |
| -26.73 |
Sun |
| -12.6 |
Full Moon |
| -8.0 |
Iridium flare (brightest) |
| -3.7 |
Venus (brightest) |
| -4.7 |
International Space Station (brightest) |
| -3.0 |
Mars (brightest) |
| -2.8 |
Jupiter (brightest) |
| -1.9 |
Mercury (brightest) |
| -1.47 |
Sirius (brightest) |
| -0.24 |
Saturn (brightest) |
| 0 |
Vega |
| 5.5 |
Uranus (brightest) |
| 6.5 |
Faintest stars observable with naked eye (perfect conditions) |
| 7.7 |
Neptune (brightest) |
| 13.65 |
Pluto (brightest) |
The original Hellenistic model (by Ptolemy and Hipparchus) of calculating magnitudes was updated and formalised in 1856 by N. R. Pogson. In Pogson’s model a first magnitude star is approximately 2.512 times as bright as a second magnitude star and so on. Vega has been selected as the standard reference star with zero magnitude.
The Hubble telescope has recorded stars of 30th magnitude in visible wavelengths and the upcoming ELT telescope (first light in 2028) will provide images 15 times sharper than those from the Hubble Space Telescope.
Surface brightness
Imagine a point source of light of given luminosity that radiates equally in all directions. An empty sphere centered on that point source will have its entire surface illuminated.
As the radius and surface of the sphere increase, given a constant point light source, a larger surface area will need to be illuminated which will lead to a decrease in observed brightness.
This is exactly what happens to celestial objects of the similar magnitude but very different surface areas, i.e., a 3.4 magnitude star versus the M31 as observed with the naked eye. Where it would be very easy to see the star, we could only be able to just see the core of the galaxy under the best conditions.
Being able to roughly estimate the surface brightness of a deep sky object rather than knowing their apparent magnitude is vital in choosing well suited targets for the imaging equipment and techniques employed.
Surface brightness is expressed in magnitude per arcsecond square. For a light source with magnitude m extending over an area of A square arcseconds, the surface brightness S can be calculated using the following formula:
S = m + 2.514 x log(A)
Most if not all planetarium software will provide information on any celestial target including their angular size.
Many sources only provide the maximum angular size of a celestial object on its longest axis which is fine for square or round shaped objects but not for other objects.
A simplified version of the above formula can be used to estimate the relative surface brightness using the maximum angular extent on one axis.
For a light source with magnitude m and maximum angular size L in arcseconds, the relative surface brightness S can be calculated using the following formula:
S = m + 2.514 x log(L x 2 x D)
Where D indicates the approximate amount of space filled by the celestial object when considering it’s the diameter of disk of space it occupies. D would be = 1 if the target was circular. To be able to calculate S you would still need to know the rough shape of the object which can be found in deep sky publications, on Google (Images) etc.
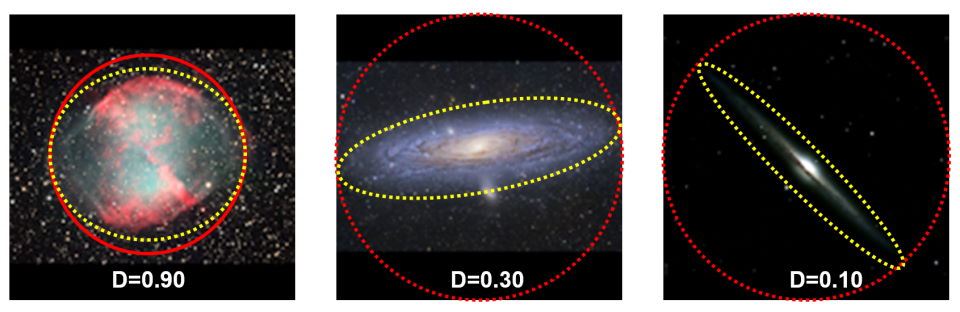
Shapes of deep sky objects.
Alternatively, we can use D=0.5 for all extended deep sky objects. This will still offer a significantly better indication of surface brightness than using apparent magnitude alone.
S = m + 2.514 x log(L x 2 x 0.5)
Related topics:
how-to guide, astrophotography, article